1、给100盏灯编号 1~100,开始时所有灯都是关着的
第1次:把所有编号是1的倍数的灯的开关状态改变一次;
第2次:把所有编号是2的倍数的灯的开关状态改变一次;
第3次,把所有编号是3的倍数的灯的开关状态改变一次;
…
第100次,把所有编号是100的倍数的灯的开关状态改变一次;
问:最后开着的灯的编号是哪些?
分析:最开始灯是灭的,因此只有经过奇数次开关状态改变,灯才会是亮的。从题意可知一个数字有多少约数就会状态改变多少次,因此这道题可以转换为:1~100数字中约数个数是奇数的有哪些。并且我们知道约数是成对出现的,如8的约数:(1,8)、(2,4),因此如果要出现约数的个数是奇数个,除非它是个平方数,如36的约数:(1,36)、(2,18)、(3,12)、(4,9)、(6),因此,这题又可以转换为1~100数字中的平方数有哪些,这操作。。。。666吧,这就是分析问题的乐趣吧
2、烧一根不均匀的绳子,从头烧到尾总共需要1小时,现在有若干条这样的绳子,问如何用烧绳子的方法来计时1小时15分钟呢
从题目知道,绳子不均匀,不能根据燃烧半根来计量半小时。但是还可以推断,从两头烧,只要半小时。因此可以使用3根绳子来计时:1)第1根绳子点燃两端,第2根绳子点燃一端,第三根绳子先不点燃; 2)第1根绳子烧完计时30分钟,接着第2根绳子另一端也点燃 3)第2根绳子烧完计时15分钟,此时已经计时45分钟了,剩下的半小时只需要将第3条绳子两端点燃就能计算出。
3、有12个外观一样的小球,但有一个与其他小球重量略微不同,用手感觉不出来,用一个天平,能称3次就能找到那个小球吗
把小球编号 1
12,然后分为3组(想想为什么是3组):14分为A组,58分为B组,912分为C组。首先A组和B组称量比较:
1、天平平衡。则目标小球在C组。将C分为两组:9、10、11分为一组C1,12分为一组C2,再从B中随意拿出3个球分组为B1,C1和B1比较:
1)若平衡,则12号球就是目标球。
2)若不平衡,则目标球在C1内,并且根据天平倾斜,可以判断目标球比普通球重还是轻(若是天平显示B1重,则目标球比较轻;反之目标球比较重),此时随意取 C1 中的2个球放在天平上即可知道结果(如果平衡,则目标球是另一个,如果不平衡,根据轻重可知目标球)。
2、天平不平衡。则目标球在A或者B中。
1)若A > B,取(1,2,3,5)为一组X,(4,9,10,11)为一组Y,(6,7,8)为一组Z,比较X和Y,若X>Y,可知不同小球在1,2,3中,且目标球重于普通球,此时再将编号 1,2,3 任取2个放上天平即可知道目标球。若X<Y,则说明4号是目标球;若X=Y,则目标球在Z中(6,7,8),并且目标球轻于普通球,此时只需要将编号 其中任意两个球放上天平即可找出目标球。
2)若 A < B,同样按照上述分为X、Y、Z三组,同理,若X<Y,则目标球在1,2,3中,且目标球轻于普通球,此时再将编号 1,2,3 任取2个放上天平即可知道目标球;若X>Y,说明4号为目标球,若X=Y,则目标球在Z中(6,7,8),并且目标球重于普通球,此时再将编号 6,7,8 任取2个放上天平即可知道目标球。
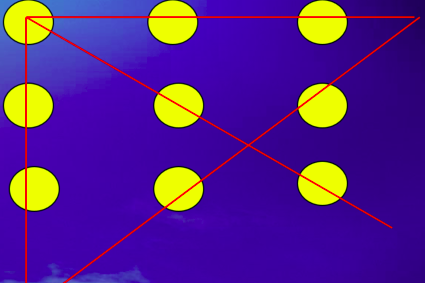
3、一笔画出经过9个点的4条直线
主要是要突破点,不要局限于点上,不说了,直接上图:
9点4线
4、有1块钱1瓶的契税,喝完后2个空瓶换一瓶汽水,问有20块钱,可以喝几瓶汽水?
总共40瓶(不要浪费最后那个空瓶,找老板借1个,凑2瓶子再喝一瓶,最后这空瓶还给老板。。。)
5、时针分针秒针重合的次数
只有2次,一次是 00:00:00 一次是 12:00:00
假设排列100个球,两个人轮流一拿球装入口袋,能拿到第100个球为胜,条件是每次拿球至少拿1个,最多拿5个,加入你是最先拿球的人,你该拿几个,以后怎么保证拿到最后一个球?
怎样保证拿到最后一个球呢?最简单的方法是最后剩下6个,并且轮到对方来拿,这样无论对方拿几个,都能保证自己拿到最后一个。
(1)首先,要控制每一轮拿出的个数,但是对方拿的个数是不受控制的,假设对方拿n个,自己就拿6-n个(为什么是控制总数是6个,是因为对手最多拿5个,自己最少能拿1个,和值就是6,自己不能把和值控制得更低;而对手至少拿1个,自己最多拿5个,同样自己不能把和值控制得更高。因此只有6才是一个可控的值)。
(2)其次,假设第一次拿x个球,以后每次自己和对方拿的和是6,最多可以拿到15轮(除去第一轮的x个,最后留这肯定少于10个了),还剩 10-x个,为了达到之前定的目标最后留6个,所以x应该是4.
(3)总结而言就是第一次拿4个,以后每次对方拿了n个后,自己拿 6-n 个。
