小黑屋

0%

面试题-算法-基础排序

发表于 更新于 分类于

冒泡排序算法

点击看答案

思路：冒泡排序基于交换排序思想。依次比较相邻的两个数，将小数放在前面，大数放在后面。

即第一趟：首先比较第1个和第2个数，将小数放前，大数放后。然后比较第2个数和第3个数，将小数放前，大数放后，如此继续，直至比较最后两个数，将小数放前，大数放后。之后便是重复第一趟步骤，直至全部排序完成(或者说直到某一趟没有发生交换的时候)。每一趟完成后，最后一个数肯定是最大的那个数，所以一次for循环后，会有 len – 操作，即每趟都比上一趟少比较一次。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
    private static void bubbleSort1(int[] ints) {
    int len = ints.length;
    boolean flag = true;
    while (flag) {
        flag = false;
        for (int i = 1; i < len; i++) {
            if (ints[i - 1] > ints[i]) {
                int temp = ints[i];
                ints[i] = ints[i-1];
                ints[i-1] = temp;
                flag = true;
            }
        }
        len -- ;
    }
}

冒泡排序在数据有序的情况下，只需要一趟即可，时间复杂度是 O(n)，在最差的情况下，每趟都有比较，时间复杂度是 O(n^2) ，平均复杂度是 O(n^2)，适合数据量较小的情况,它是稳定的排序方法，

选择排序

点击看答案

选择排序的基本思想：每次从待排序的数据元素中选出最小(大)的一个元素，放在序列的起始位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public static void selectSort(int[] a){
    for (int i = 0; i< a.length - 1; i++){
    
        int index = i;//当前趟最小的数所在index
        
        for (int j=i+1; j < a.length; j++){
            if (a[j] < a[index]){
                index = j;
            }
        }
        
        if (index != i){
            int temp = a[i];
            a[i] = a[index];
            a[index] = temp;
        }
    }
}

它的时间复杂度是O(n^2)，因为它总是要循环那么多次，并且每次都是从待排序的数据中挑选最小的，因此它是不稳定的排序算法。

插入排序

点击看答案 插入排序的原理类似于打牌的时候抓牌，每次抓牌上来，都按照顺序将其插入到之前排好序的牌堆中。 
1
2
3
4
5
6
7
8
9
10
11
public void doInsertSort(){
    for(int index = 1; index<length; index++){//外层向右的index，即作为比较对象的数据的index
        int temp = array[index];//用作比较的数据
        int leftindex = index-1;
        while(leftindex>=0 && array[leftindex]>temp){//当比到最左边或者遇到比temp小的数据时，结束循环
            array[leftindex+1] = array[leftindex];
            leftindex--;
        }
        array[leftindex+1] = temp;//把temp放到空位上
    }
}

时间复杂度是O(n^2)，适用于数据量较少的情况，是稳定的排序。

shell排序

点击看答案 原理： 严格来说是基于插入排序的思想，shell排序有点不大好理解，后续再看看 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/**
 * 思路：三层循环
 * 第一层循环：控制增量-增量随着程序的进行依次递减一半
 * 第二层循环：遍历数组
 * 第三层循环：比较元素，交换元素。
 * 这里需要注意的是：比较的两个元素和交换的两个元素是不同的。
 */
public static shellSort(int[] data) {
    for (int div = data.length/2; div>0; div/=2) {
        for (int j = div; j < data.length; j++) {
            int temp = data[j];
            for (int k=j; k>=div && temp<data[k-div] ; k-=div) {
                data[k] = data[k-div];
            }
            data[k] = temp;
        }
    }
}

shell排序最差的时间复杂度是 O(n^2)，平均复杂度是 O(nlogn)，是不稳定的排序

快速排序

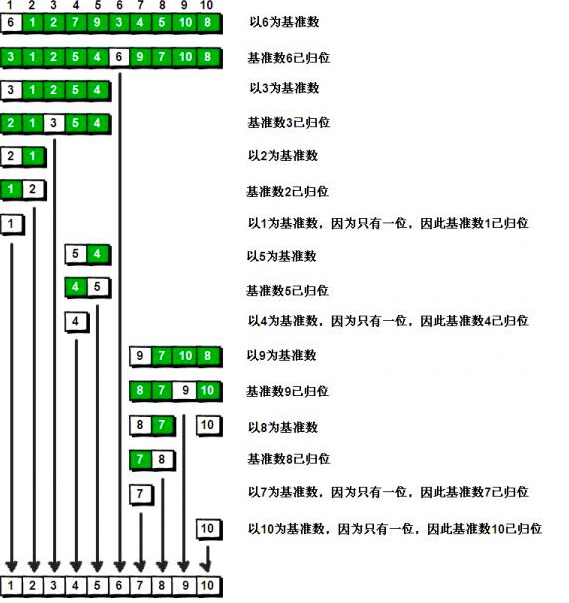
点击看答案

快速排序的思想是分治思想。假设我们现在对“6 1 2 7 9 3 4 5 10 8”这10个数进行排序。首先在这个序列中随便找一个数作为基准数，为了方便，就让第一个数6作为基准数吧。接下来，需要将这个序列中所有比基准数大的数放在6的右边，比基准数小的数放在6的左边。得到一个一个以6为中心的序列，再以6为界限，将左右两边都看成数组，分别按照刚才的方法排序。上个图会比较直观：

快速排序

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
public static void quickSort(int[] arr,int low,int high){
    int i,j,temp,t;
    if(low>high){
        return;
    }
    i=low;
    j=high;
    //temp就是基准位
    temp = arr[low];
 
    while (i<j) {
        //先看右边，依次往左递减
        while (temp<=arr[j]&&i<j) {
            j--;
        }
        //再看左边，依次往右递增
        while (temp>=arr[i]&&i<j) {
            i++;
        }
        //如果满足条件则交换
        if (i<j) {
            t = arr[j];
            arr[j] = arr[i];
            arr[i] = t;
        }
 
    }
    //最后将基准为与i和j相等位置的数字交换
     arr[low] = arr[i];
     arr[i] = temp;
    //递归调用左半数组
    quickSort(arr, low, j-1);
    //递归调用右半数组
    quickSort(arr, j+1, high);
}

快排的平均时间复杂度是 O(nlogn) ，最坏情况下为 O(n^2)，这种交换方式导致它是不稳定的排序。

堆排序

点击看答案

堆排序是一种选择排序。

堆排序时，先构建堆(假设大顶堆)，将数组转换成堆，数据在堆中是按层编号的，所以数组中一个编号为 i 的结点的子结点在 2i + 1 和 2i + 2 的位置。开始构建时，首先从最后一个非叶子结点开始(叶子结点不用调，叶子结点只是非叶子结点比较时被动移动)，最后一个非叶子节点的位置在 n/2-1。

构建了大顶堆后，堆顶元素与末尾元素交换，将大元素“沉”到末尾，将除尾部以外的元素再构建大顶堆，如此循环，每次找到最大的下沉的后面。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
private static void heapSort(int[] arr){
    int arrLen = arr.length;
    int temp;
    
    //建立大顶堆
    for (int i = arrLen/2 -1;i>=0;i--){
        //从第一个非叶子结点(在 arrLen/2 -1 处)从下至上，从右至左调整结构
        adjustHeap(arr,i,arrLen);

    }

    for (int j = arrLen -1;j >= 0;j--){
        //将堆顶元素与末尾元素进行交换
        temp = arr[0];
        arr[0] = arr[j];
        arr[j] = temp;
        
        //重新对堆进行调整
        adjustHeap(arr,0,j);
    }
}

private static void adjustHeap(int[] arr,int start,int end){
    //先取出当前元素i
    int temp = arr[start];

    for (int k = 2*start + 1;k < end;k = 2*k + 1){//从i结点的左子结点(2i+1处)开始
        if (k + 1 < end && arr[k] < arr[k + 1]){//如果左子结点小于右子结点，k指向右子结点
            k ++;
        }
        
        //如果子节点大于父节点，将子节点值赋给父节点（不用进行交换）
        if (arr[k] > temp) {
            arr[start] = arr[k];
            start = k;
        }else {
            break;
        }
    }

    //将temp值放到最终的位置
    arr[start] = temp;
}

它的最坏，最好以及平均复杂度都是 O(nlogn)，它是不稳定排序。

以上内容参考自他人的博客

归并排序

点击看答案

归并排序是基于 分治法 实现的。目前还看不大懂，后续再理解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
    //非递归算法实现二路归并排序，length代表数组长度，即数组最大下标是 legth - 1
void mergeSort(int List[],int length){
    int size = 1;
    int low;
    int mid;
    int high;
    //size 是标记当前各个归并序列的high-low，从1，2，4，8，……，2*size
    while(size <= length - 1){
        //从第一个元素开始扫描，low代表第一个分割的序列的第一个元素
        low = 0;
        //当前的归并算法结束的条件
        while(low + size <= length - 1){
            //mid代表第一个分割的序列的最后一个元素
            mid = low + size - 1;
            //high 代表第二个分割的序列的最后一个元素
            high = mid + size;
            //判断一下：如果第二个序列个数不足size个
            if(high > length - 1){
                //调整 high 为最后一个元素的下标即可
                high = length - 1;
            }
            //调用归并函数，进行分割的序列的分段排序
            merge(List, low, mid, high);
            //打印出每次归并的区间
            cout << "low:" << low << " mid:" << mid << " high:" << high << endl;
            //下一次归并时第一序列的第一个元素位置
            low = high + 1;
        }// end of while
        //范围扩大一倍，二路归并的过程
        size *= 2;
    }
}

归并的思想主要用于外部排序：
外部排序可分两步
①待排序记录分批读入内存，用某种方法在内存排序，组成有序的子文件，再按某种策略存入外存。
②子文件多路归并，成为较长有序子文件，再记入外存，如此反复，直到整个待排序文件有序。

总结

上述排序，稳定的排序有：冒泡、插入、合并 ，不稳定排序：选择、shell、快排、堆排

谢谢你的鼓励