小黑屋

0%

面试题-算法-概念

发表于 更新于 分类于

二叉查找树(也称二叉搜索树)

  • 左子树上的节点值都小于等于根节点的值
  • 右子树上的节点值都大于等于根节点的值
  • 左右子树也是二叉搜索树

它是基于二分查找的思想，查找最大的次数为二叉树高度

查找代价

  • 当左右子树高度大致平衡时，时间复杂度在 O(logN)
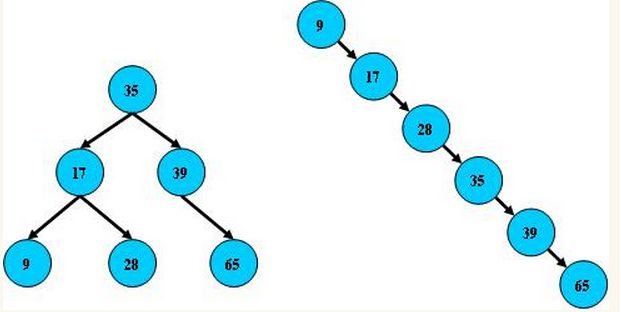
  • 当先后插入的关键字有序时，退化成链表，查找的时间复杂度就在 O(N)了

插入代价

新节点插入到树的叶子节点上，因此，插入节点和查找一个不存在的数据的代价相同

删除代价

  • 如果被删除的节点左、右 有一个为null时，代价仅为 O(1)
  • 如果左右子树都存在，时间复杂度最大也不会超过O(logN)

缺陷：

极端情况可能退化成链表，时间复杂度为 n。这主要是由于树不平衡导致的

平衡二叉查找树(平衡二叉搜索树)

是严格的平衡二叉树，它是空树或者左右两个子树的高度差 小于等于1，同时，左右两个子树也是平衡二叉搜索树

查找代价

时间很稳定，查找效率最好最坏都是 O(logN)

插入代价

由于要保证严格的平衡，插入时可能要进行再平衡(最多旋转一次)，因此插入的整体代价还在 O(logN)

删除代价

和插入一样，要考虑再平衡，但是最多需要O(logN)次旋转，所以时间复杂度为 O(2logN)

红黑树(Red-Black Tree)

它并不严格地平衡，最长路径长度不超过最短路径长度的2倍。它删除和插入引起平衡性改变的概率要远低于平衡二叉搜索树

查找代价

查找代价基本上维持在 O(logN) 级别，最差情况下肯定比平衡二叉搜索树要差，因为没有那么平衡

插入代价

不容易引起失衡，整体代价和平衡二叉搜索树差不多，也是 O(logN) 级别(虽然涉及变色，但是变色的代价很小)

删除代价

相对平衡二叉搜索树，不容易引起失衡，时间复杂度也在 O(logN) 级别

补充

平衡二叉搜索树由于插入和删除，会引起需要调整，可以通过 ：变色、左旋转、右旋转 三种方式调整。是否需要调整要根据红黑树的特性：

  • 节点是红色或黑色
  • 根节点是黑色
  • 叶子节点都是黑色的空节点
  • 红色节点的两个子节点都是黑的(红节点不能连续出现)
  • 任一点到每个叶子节点的路径包含相同数目的黑节点

以上内容参考自zhihu、csdn、知乎

B-树和B+ 树

我们所谓的B-树，其实并不是B减树，中间是横线，不是减号；B + 就是 B加树了

如 os 的文件目录存储、数据库中的索引结构的存储，不可能在内存中建立查找结构，必须在磁盘中建立好结构。

在磁盘组织结构下，从任何一个节点指向其他节点都可能读取一次磁盘，再将数据写入内存比较。这回带来大量的IO操作，所以我们需要新的数据结构，即 B树和B+树。

B树是一种多路平衡查找树，每个节点最多包含k个孩子，k称为B树的阶。K大小取决于磁盘页的大小。

一些算法上的概念

B树

理解平衡二叉树后，就会更好理解后续的B树。

平衡二叉树

平衡二叉树是一棵二叉树，每个节点的左边节点小于当前节点的值，右边节点的值大于当前节点的值。

因为二叉树的遍历性能和树的层级成反比，层级h越小查询越快，为了保证树的结构左右两端数据大致平衡以降低二叉树高度，一般会采用算法机制实现节点的平衡，如下图所示：

平衡树的高度

B 树

当上述的平衡二叉树深度很深无法存储所有的节点数据时，需要读取磁盘。从而树的深度越大，需要的I/O操作次数越多，因此效率也越低，因此我们需要想办法降低树的高度。

B 树的思路和平衡二叉树一样，但是采用了多叉的方式降低了高度。

B树的具体实现比较难描述，看下面的参考链接更清晰，就不赘述。

以上内容参考自： 勤劳的小手、B树概念

字符串匹配

主要是利用KMP算法，这个很令人头大，这里贴出算法代码，如果需要详细了解，可以去查看July大神的这篇文章。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public static int kmp(String str, String dest,int[] next){//str文本串  dest 模式串
        for(int i = 0, j = 0; i < str.length(); i++){
            while(j > 0 && str.charAt(i) != dest.charAt(j)){
                j = next[j - 1];
            }
            if(str.charAt(i) == dest.charAt(j)){
                j++;
            }
            if(j == dest.length()){
                return i-j+1;
            }
        }
        return 0;
    }
    public static int[] kmpnext(String dest){
        int[] next = new int[dest.length()];
        next[0] = 0;
        for(int i = 1,j = 0; i < dest.length(); i++){
            while(j > 0 && dest.charAt(j) != dest.charAt(i)){
                j = next[j - 1];
            }
            if(dest.charAt(i) == dest.charAt(j)){
                j++;
            }
            next[i] = j;
        }
        return next;
    }

next数组的计算主要跟模式串有关，与文本串并没有关系，因为，模式串前后公共最长子序列。这样才会让我们跳过大量的重复计算

数字排列

题目：用1，2，2，3，4，5 这6个数字，写一个方法，打印出所有不同的排列，如 512234、412235等，要求4不能再第三位，3与5不能相连。

思路：问题可以归结为图的遍历，实际上6个数字就是6个结点，把6个结点连成无向连通图，对于每个结点求这个图形的遍历路径，所有结点的遍历路径就是最后对这6个数字的排列组合结果集。当然，这样获取的结果集未达到题目要求：
（1）3与5不能相连，这个可以在构造图的时候就满足条件；
（2）不能重复，有两个2，明显会存在重复结果，得最后去重（可以放在treeSet中）；
（3）4不能排在第三位，这个仍旧在结果集中排除即可。

具体代码略。

手写算法题。猫扑素数；1到n，求1的个数；单词反转。

算法：排序、二叉树遍历、红黑树了解。常见的数据结构主要有数组、链表、栈、队列、二叉堆、树、图等，红黑树和BL树的区别

快速排序底层原理简单描述。

谢谢你的鼓励